【講義】おうぎ形の弧の長さと面積
- 正解率:9.09%
- 解答数:11
EXAMPLE
例題
次のようなおうぎ形の弧の長さと面積を求め,ア~カに当てはまる数を半角英数字で入力しなさい。
- 半径4cm,中心角60°
- 半径5cm,中心角144°
TEXT
テキスト解説
次の図のように,おうぎ形は円の一部分です。そこで,中心角が360度になっているおうぎ形が円であると考えると,中心角が
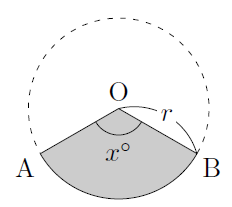
このことから,半径
このとき,おうぎ形の弧の長さを
のように表され,おうぎ形の面積は,底辺
MOVIE
動画解説
次のようなおうぎ形の弧の長さと面積を求め,ア~カに当てはまる数を半角英数字で入力しなさい。
次の図のように,おうぎ形は円の一部分です。そこで,中心角が360度になっているおうぎ形が円であると考えると,中心角が

このことから,半径
このとき,おうぎ形の弧の長さを
のように表され,おうぎ形の面積は,底辺