【講義】ひし形
EXAMPLE
例題
平行四辺形ABCDで,
TEXT
テキスト解説
4つの辺が等しい四角形(定義)をひし形といい,次の図のようなひし形では,
となります。
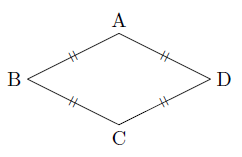
このとき,
のように表すことができるので,ひし形は,「2組の向かい合う辺が等しい四角形」になります。つまり,ひし形は平行四辺形の特別なものと考えることができるので,次の平行四辺形の定義や定理はすべて,ひし形でも成り立ちます。
- 2組の向かい合う辺がそれぞれ平行
- 2組の向かい合う辺はそれぞれ等しい
- 2組の向かい合う角はそれぞれ等しい
- 対角線はそれぞれの中点で交わる
また,平行四辺形は次の各場合にひし形になります。
- 1組の隣り合う2辺が等しいとき
- 対角線が垂直であるとき
MOVIE
動画解説
