下の図の直線(1)，(2)は，それぞれある1次関数のグラフになります。これらの関数の式を求め，ア～キに当てはまる数を半角英数字で入力しなさい。ただし，${\displaystyle -\frac{1}{2}}$のような分数は，${\displaystyle \frac{-1}{2}}$のように分子に符号を含む形で入力すること。

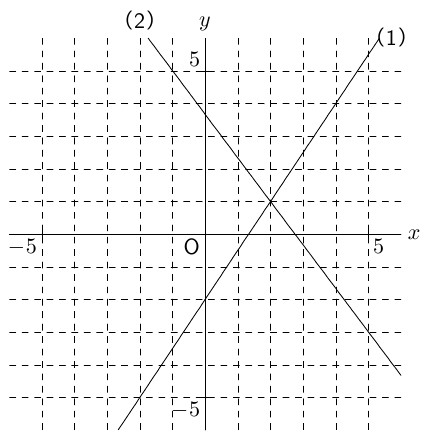
1. ${\displaystyle y=\frac{\boxed{\text{ア}}}{\boxed{\text{イ}}}x-\boxed{\text{ウ}}}$
2. ${\displaystyle y=\frac{\boxed{\text{エ}}}{\boxed{\text{オ}}}x+\frac{\boxed{\text{カ}}}{\boxed{\text{キ}}}}$

1次関数のグラフは直線になるので，それとは逆にグラフが直線になっていれば，1次関数のグラフであると判断できます。1次関数の式は，

1. 直線の傾きと通る点の座標
2. 直線の通る2点の座標

がわかれば求めることができるので，そのいずれかをグラフから読み取ることになります。しかし，グラフから直線の傾きを読み取るためには，直線の通る2点の座標が必要になるので，グラフから読み取りやすい直線の通る適当な2点を選び，1次関数の式を求めることになります。