下の図で，$\angle{x}$，$\angle{y}$の大きさを求め，ア，イに当てはまる数を半角英数字で入力しなさい。

\[ \angle{x} = \fbox{ア}^{\circ}, \quad \angle{y} = \fbox{イ}^{\circ} \]

多角形の1辺と，その1辺と隣り合う辺の延長とが作る角を外角といい，多角形の隣り合った2辺が作る，多角形の内側に向いた角を内角といいます。

次の図のように，△ABCの辺BCを延長した直線上に点D，辺ACを延長した直線上に点Eをとります。

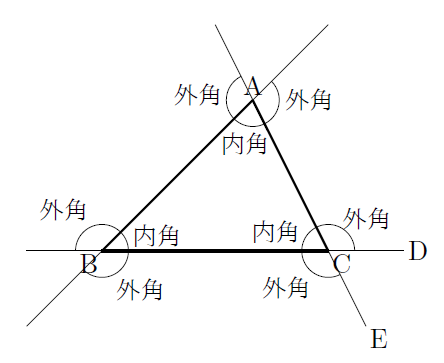
このとき，∠ACD，∠BCEを，△ABCの頂点Cにおける外角といい，同じようにして，頂点A，Bにおける外角も考えることができます。また，外角に対して，△ABCの3つの角∠A，∠B，∠Cを内角といいます。

今度は次の図のように，△ABCの辺BCを延長した直線上に点Dをとり，点Cを通り辺BAに平行な直線をCEにします。

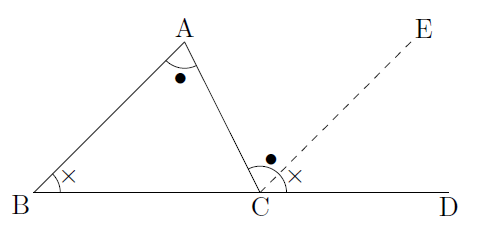
このとき，BA//CEより，平行線の同位角，錯角は等しいので，

\[ \angle{\text{A}} = \angle{\text{ACE}}, \quad \angle{\text{B}} = \angle{\text{ECD}} \]

となります。また，一直線のつくる角は$180^{\circ}$であるので，

\begin{align}
\angle{\text{A}} + \angle{\text{B}} + \angle{\text{C}} &= \angle{\text{ACE}} + \angle{\text{ECD}} + \angle{\text{C}} \\
&=\angle{\text{BCD}} = 180^{\circ}
\end{align}

となり，このことから，「三角形の3つの内角の和は$180^{\circ}$」ということがわかります。

また，

\[ \angle{\text{ACD}} = \angle{\text{ACE}} + \angle{\text{ECD}} = \angle{\text{A}} + \angle{\text{B}} \]

より，「三角形の1つの外角は，その隣にない2つの内角の和に等しい（外角の定理）」ということもわかります。