次の計算をし，ア～エに当てはまる数を半角英数字で入力しなさい。

1. \( (+9) +(+13) = \fbox{ア} \)
2. \( (-9) +(-4) = \fbox{イ} \)
3. \( (+12) +(+4) = \fbox{ウ} \)
4. \( (-1) +(-12) = \fbox{エ} \)

足し算は，「数を加える計算方法」ということで加法（かほう）といい，加法で計算した結果のことを和といいます。それに対し引き算は，「数を減らす計算方法」ということで減法（げんぽう）といい，減法で計算した結果のことを差といいます。そして，加法と減法を略して「加減」ということもあります。また，2つの数の符号が同じことを同符号といい，ここでは，同符号の2数の和について考えます。

(i)同符号（+）の2数の和：\( (+2)+(+3) \)

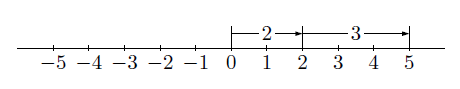
「\( (+2) +(+3) \)」は，数直線の0（原点）を基準に，正の方向に「2」だけ移動し，さらに，正の方向に「3」移動することを意味するので，

\[ (+2) +(+3) =+(2 +3) =+5 \]

(ii)同符号(-)の2数の和：\( (-2) +(-3) \)

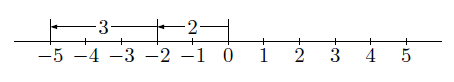
「\( (-2)+(-3) \)」は，数直線の0（原点）を基準に，負の方向に「2」だけ移動し，さらに，負の方向に「3」移動することを意味するので，

\[ (-2) +(-3) =-(2 +3) =-5 \]

以上のことから，同符号の2数の和は，「\( (+2) +(+3) \)」は2つとも正の方向に，「\( (-2) +(-3) \)」は2つとも負の方向といったように，数直線上で同じ方向に動きます。そのため，どれだけ原点からはなれたかを，2数の絶対値の和を計算することで求め，正か負かは2数と同じ符号になるので，そのことでどの位置に移動したかが判断できることになります。つまり，2数の絶対値の和を求め，2数と同じ符号をつけることで計算できます。