【講義】回転移動
EXAMPLE
例題
次の図のような△ABCがあります。点Bを中心として左回り(反時計回り)に
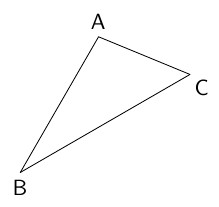
TEXT
テキスト解説
用紙に何か図をかき,その用紙の1点を画びょうなどでとめて用紙を動かすと,図が移動します。このように,ある図形を,ある点を中心として一定の角度だけ回転する移動を回転移動といいます。
次の図のように,△ABCを点Oを中心に回転移動させて,△A’B’C’になるとき,点Oを回転の中心といいます。
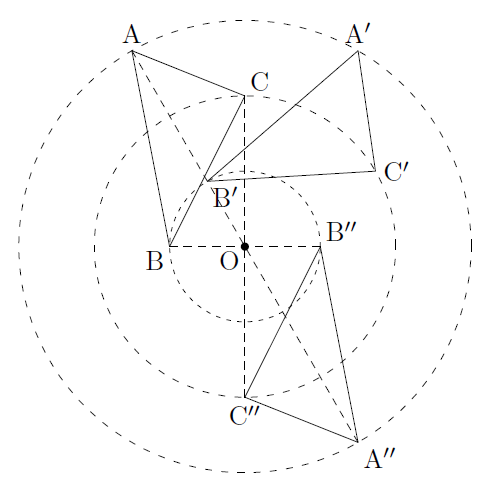
このとき,図形上のすべての点が回転の中心Oを中心とする同じ円周上を同じ角度だけ動きます。つまり,それぞれ対応する点は,回転の中心から等しい距離になり,
という関係が成り立ち,また,対応する点を,回転の中心Oと結んでできる角(回転角)はすべて等しく,
という関係も成り立ちます。
そして,△ABCを点Oを中心に回転角が180度になるような回転移動(△A”B”C”)を特に,点対称移動といい,回転の中心Oを対称の中心といいます。このとき,△ABCと△A”B”C”は点Oを中心として対称である,または,点対称であるといいます。
MOVIE
動画解説
