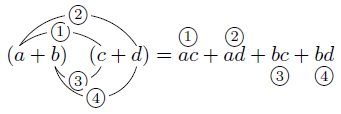次の式を展開し，ア～オに当てはまる数を半角英数字で入力しなさい。

1. \( (2x +1)(x +3) =\fbox{ア}x^2 +\fbox{イ}x +\fbox{ウ} \)
2. \( (3x +5y)(2x -3y) =\fbox{エ}x^2 +xy -\fbox{オ}y^2 \)

積の形で書かれた式を計算して単項式の和の形に書き表すこと（1つの多項式で表すこと）を，もとの式を展開するといいます。つまり，「かっこをはずしてバラバラにする」ことです。また，積の記号「\( \times \)」は，

\[ x \times y \longrightarrow x \cdot y \]

のように，記号「\( \cdot \)」を用いて省略して表すこともあります。

\( (a +b)(c +d) \)のような「\( \textbf{（多項式）} \times \textbf{（多項式）} \)」を展開するには，主に次のような2つの方法があります。

1. まとまりを1つのものと考える
2. かっこの中に含まれるすべての項を分配する

そこで，この2つの展開の方法で\( (a +b)(c +d) \)を展開してみます。

1. 「\( a +b \)」または「\( c +d \)」をひとまとまりにして展開する。
1. \( a +b=A \)とすると，
   \[ (a +b)(c +d) =A \times (c+d) \]
   という形に変形でき，こうすることで「\( \textbf{（単項式）} \times \textbf{（多項式）} \)」の形になります。そこで，分配法則を利用して，
   \[ A \times (c +d) =A \times c +A \times d \]
   となります。ここで，\( A \)を元に戻してあげると，
   \[ A \times c +A \times d =(a +b) \times c +(a +b) \times d \]
   となり，さらに「\( \textbf{（多項式）} \times \textbf{（単項式）} \)」という形が出てくるので，再度分配法則を用いて，
   \begin{align}
   (a +b) \times c +(a +b) \times d &=a \times c +b \times c +a \times d +b \times d \\
   &=ac +bc +ad +bd
   \end{align}
   となります。
2. \( c +d =B \)とすると，
   \[ (a +b)(c +d) =(a +b) \times B \]
   という形に変形でき，こうすることで「\( \textbf{（多項式）} \times \textbf{（単項式）} \)」の形になります。よって，分配法則を利用して，
   \[ (a +b) \times B =a \times B +b \times B \]
   となります。ここで，\( B \)を元に戻してあげると，
   \[ a \times B +b \times B =a \times (c +d) +b \times (c +d) \]
   となり，「\( \textbf{（単項式）} \times \textbf{（多項式）} \)」という形が出てくるので，再度分配法則を用いて，
   \begin{align}
   a \times (c +d) +b \times (c +d) &=a \times c +a \times d +b \times c +b \times d \\
   &=ac +ad +bc +bd
   \end{align}
   となります。
2. 1の結果から，結局
   
   のように，多項式の各項を順に分配して積を作り，その和を考えればよいことになります。これは，\( (a +b) \times (c +d) \)を
   \[ \textbf{たての長さ：}a +b, \ \ \ \ \ \textbf{横の長さ：}c +d \]
   である長方形の面積であると考えて，次の図のように長方形を4つに分割し，それぞれの長方形の面積の和が全体の面積になることから，
   \[ (a +b)(c +d) =ac +ad +bc +bd \]
   になるのだと考えると，イメージがしやすいと思います。

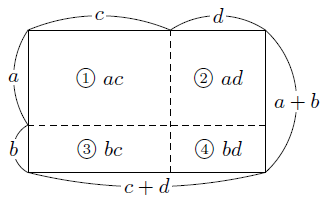
展開した計算結果は，降べきの順で整理するよう心がけてください。