【講義】対頂角
- 正解率:71.43%
- 解答数:7
EXAMPLE
例題
次の図で,
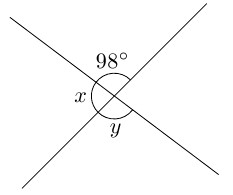
TEXT
テキスト解説
2本の直線が交わると,次の図のように4つの角ができます。
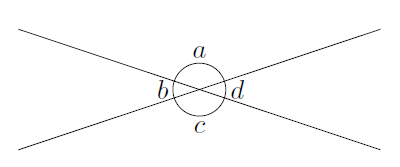
このとき,
ここで,直線の作る角は
となり,①,②より次の関係が成り立ちます。(図でも確認してみましょう。)
同じようにして,
となるので,③,④より次の関係が成り立ちます。
以上のことから,
となることがわかるので,「対頂角は等しい」という性質があります。
MOVIE
動画解説
次の図で,

2本の直線が交わると,次の図のように4つの角ができます。

このとき,
ここで,直線の作る角は
となり,①,②より次の関係が成り立ちます。(図でも確認してみましょう。)
同じようにして,
となるので,③,④より次の関係が成り立ちます。
以上のことから,
となることがわかるので,「対頂角は等しい」という性質があります。