【講義】平行線と同位角・錯角・同側内角
- 正解率:52.28%
- 解答数:197
EXAMPLE
例題
次の図で,
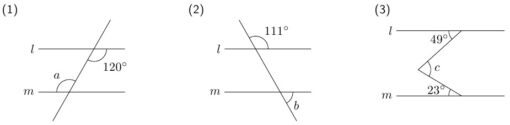
TEXT
テキスト解説
平行な2直線に1直線が交わるとき,次の図のように,同位角や錯角はそれぞれ等しくなります。

また,これとは逆に,2直線が1直線に交わるとき,
- 同位角が等しければ(
- 錯角が等しければ(
となり,これが「2直線が平行になるための条件」になります。
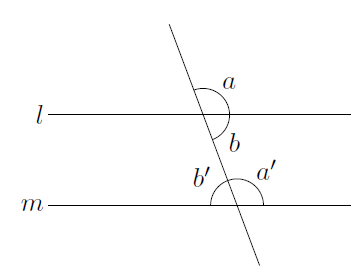
そして,次の図のように,平行な2直線に1直線が交わるとき,直線の作る角は
これと①の関係から,
という関係が成り立ち,平行な2直線に1直線が交わるとき,「同側内角の和は
MOVIE
動画解説
