【講義】直線上にある点を通る垂線
EXAMPLE
例題
下の図のような線分ABがあります。線分ABを1辺とする正方形(すべての辺の長さが等しく,すべての角の大きさの等しい四角形)を1つ作図しなさい。

TEXT
テキスト解説
次の図のような直線
ここで,図のように直線
になります。直線
になることから,点Pを通る直線
そこでまず,点Pを中心とする円をかき,直線
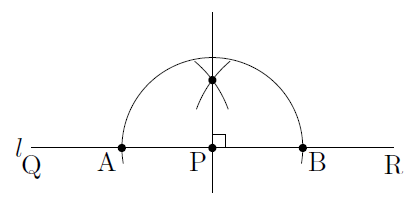
以上のことから,次の手順により垂線を作図することができます。
- 基準となる点を中心とする円をかく
- 円と直線との交点を中心とする等しい半径の円をかく
- 2つの円の交点と基準となる点を結ぶ直線を引く
MOVIE
動画解説
