【講義】重複順列
- 正解率:100.00%
- 解答数:2
EXAMPLE
例題
次の問いについて,アに当てはまる数を半角英数字で入力しなさい。
1と2の2つの数字があります。この2つの数字を使って5けたの整数を作るとき,全部で
TEXT
テキスト解説
異なる

と表されますが,同じものを繰り返し使うことが許される重複順列の場合,1番目が
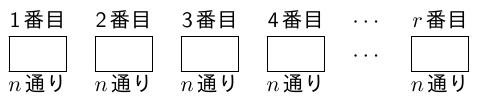
と表されます。
MOVIE
動画解説
次の問いについて,アに当てはまる数を半角英数字で入力しなさい。
1と2の2つの数字があります。この2つの数字を使って5けたの整数を作るとき,全部で
異なる

と表されますが,同じものを繰り返し使うことが許される重複順列の場合,1番目が

と表されます。