【講義】1次関数のグラフ
EXAMPLE
例題
1次関数
について以下の問いに答えなさい。
(i) 下のような

(ii) (i)の表から,それらに対応する点
TEXT
テキスト解説
1次関数
となることによって,

このことから,1次関数
となるので,1次関数
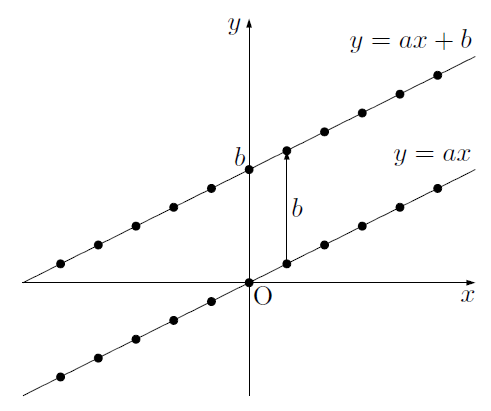
このように,1次関数
MOVIE
動画解説
1次関数
について以下の問いに答えなさい。
(i) 下のような

(ii) (i)の表から,それらに対応する点

1次関数
となることによって,

このことから,1次関数
となるので,1次関数

このように,1次関数