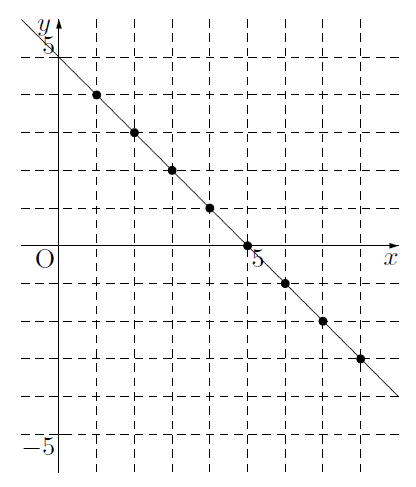
2元1次方程式を満たす,の組は,次のようになります。
このとの組を座標とする点を図に表してみると次の図のようになり,,の組をもっと細かく,
のようにして考えていくと,そのとの組を座標とする点を図に表したとき,それらの点が集まって図のような直線に近づきます。

このようにして,2元1次方程式の解となる点の全体は,1次関数のグラフと一致し,この直線を方程式のグラフといいます。
,,を定数とするとき,2元1次方程式(ただし,)をについて解くと,
と変形でき,,とすると,②の式は,と表すことができます。つまり,2元1次方程式をについて解くと,1次関数の形に変形することができるので,()のグラフは直線になります。
このときであるとすると,②の式はとなり,の値にかかわらず常にの値がであることを表しています。この方程式をグラフにすると,次の図のように点を通り,軸に平行な直線になります。

また,,のとき,①の式は,となり,の値にかかわらず常にの値がであることを表しています。この方程式をグラフにすると,上の図のようにを通り,軸に平行な直線になります。
このことから,という方程式のグラフは軸,という方程式のグラフは軸になります。