【解説】
次の図のように,△ABCの頂点A,B,Cと,この三角形の辺やその辺の延長上にない点Oとを結ぶ直線が,対辺またはその延長と交わる点をそれぞれP,Q,Rとします。
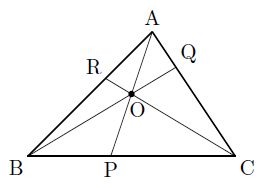
このとき,次のような底辺の等しい2つの三角形をそれぞれ選ぶと,面積比は高さの比に等しくなるので,次のように表すことができます。
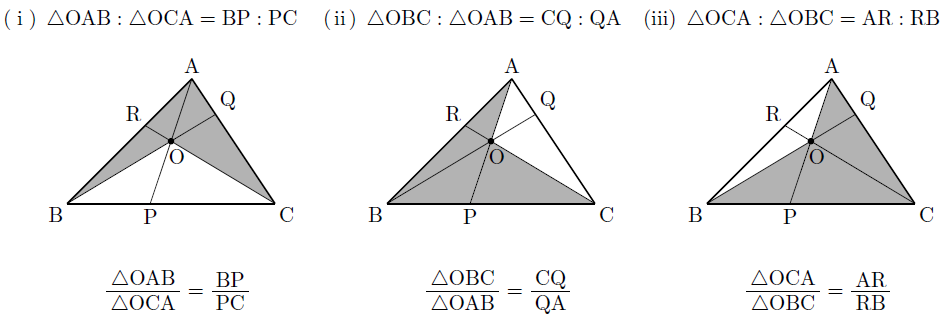
このことから,
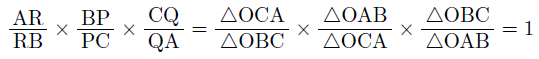
という関係が成り立ち,これをチェバの定理といいます。
【例題】

【無料動画講義(理論)】
【演習問題】

次の図のように,△ABCの頂点A,B,Cと,この三角形の辺やその辺の延長上にない点Oとを結ぶ直線が,対辺またはその延長と交わる点をそれぞれP,Q,Rとします。

このとき,次のような底辺の等しい2つの三角形をそれぞれ選ぶと,面積比は高さの比に等しくなるので,次のように表すことができます。

このことから,
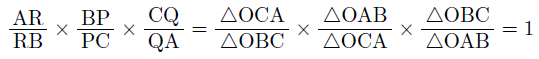
という関係が成り立ち,これをチェバの定理といいます。

