【解説】
次の図のように,直角三角形の直角をはさむ2辺の長さをa,b,斜辺の長さをcとし,∠A=x,∠B=yとします。
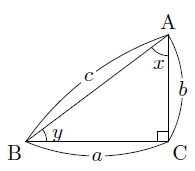
三角形の内角の和は180°であるので,
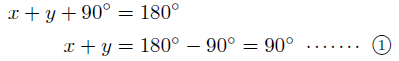
となります。
ここで,この直角三角形を4つ使って,次の図のような正方形ABCDを作ります。
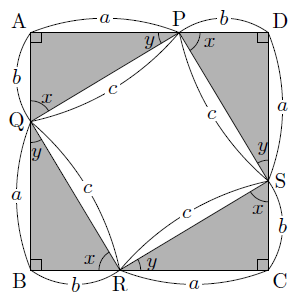
この正方形ABCDは,1辺の長さがa+bの正方形なので,その面積は次のように表すことができます。
正方形ABCD=(a+b)2……②
ここで,∠BRCは一直線の作る角で180°なので,
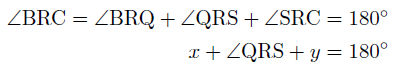
となります。
①の関係から,この式はさらに
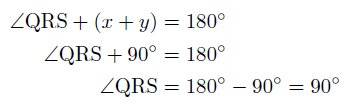
となるので,四角形PQRSは1辺の長さcの正方形になります。
すると,正方形ABCDは,4つの直角三角形と,1辺の長さcの正方形でできていると考えることができるので,その面積は
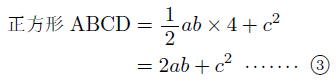
と表すことができます。
以上のようにして,正方形ABCDの面積を2つの方法で表すことができたので,②,③より,
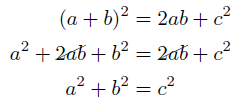
という式を導くことができます。
このことから,直角三角形の3辺の長さの間に,
a2+b2=c2
という関係が成り立ち,これを三平方の定理といいます。つまり,三平方の定理とは,
「直角をはさむ2辺の平方の和は,斜辺の平方と等しくなる」
というものになります。
【例題】

