三平方の定理の逆

【解説】

図のような3辺の長さで，a²+b²=c²である△ABCと，∠R=90°である△PQRがあります。

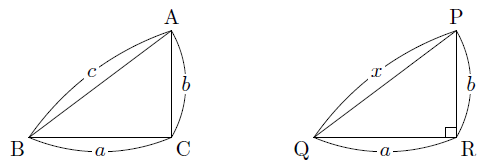
△PQRは∠R=90°の直角三角形であるので，三平方の定理より，

a²+b²=x²……①

また，仮定より，

a²+b²=c²……②

であるので，①，②より

x²=c²

xもcも辺の長さであるので，

x>0，c>0より　x=c

よって，△ABCと△PQRは，3辺の長さがそれぞれ等しいので，

△ABC≡△PQR

合同な図形の対応する角の大きさは等しいので，

∠C=∠R=90°

となります。

このことから，次の図のような△ABCで，BC=a，CA=b，AB=cとするとき，△ABCが∠C=90°の直角三角形であれば，

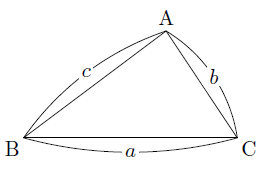
a²+b²=c²

という三平方の定理が成り立ちましたが，これとは逆に，△ABCで，

a²+b²=c²ならば∠C=90°

という関係が成り立つことになります。