中点連結定理

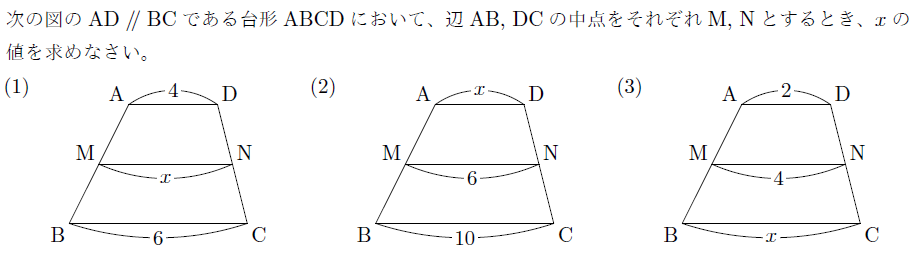
【解説】

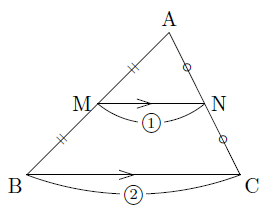
次の図のように，△ABCの2辺AB，ACの中点をそれぞれM，Nとします。

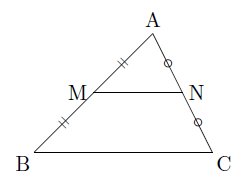
このとき，△AMNと△ABCで，M，Nは辺AB，ACの中点なので，

AM:AB=1:2……①，AN:AC=1:2……②

①，②より，

AM:AB=AN:AC=1:2……③

また，∠Aは2つの三角形に共通な角なので，

∠MAN=∠BAC……④

③，④より，2組の辺の比とその間の角がそれぞれ等しいので，

△AMN∽△ABC

相似な図形の対応する角は等しいので，

∠AMN=∠ABC

このことから，同位角が等しいので

MN//BC

また，相似な図形の対応する辺の長さの比も等しいので，

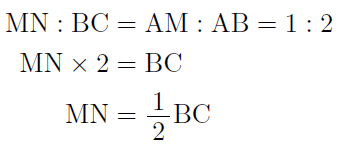
となります。

このように，△ABCの2辺AB，ACの中点をそれぞれM，Nとすると，線分MNと線分BCの間に，

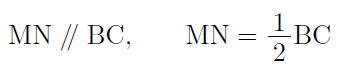
という関係が成り立ち，これを中点連結定理といいます。