【解説】
三角形は外接円を作図することができるので,必ず円に内接します。そのため,四角形ABCDの3つの頂点A,B,Cを通るような円を作図することはできますが,次の図のように残りの頂点Dも円周上にあるとは限らないので,四角形の場合は必ず円に内接するとはかぎりません。
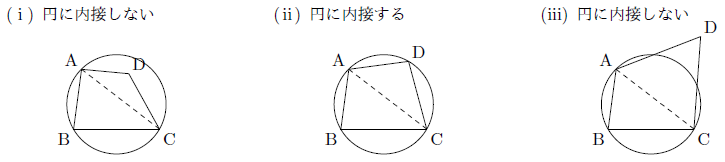
そこで,四角形が円に内接する条件(共円条件)について考えます。
次の図のような四角形ABCDにおいて,
∠B+∠D=180°……①
であるとします。
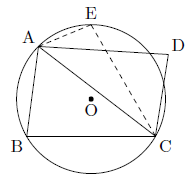
また,△ABCの外接円をかき,これを円Oとします。さらに,ACに対してBと反対側の円周上に点Eをとります。
このとき,四角形ABCEは円Oに内接するので,対角の和は180°になり,
∠B+∠E=180°……②
①,②より
∠D=∠E
点D,Eは直線ACに対して同じ側にあるので,円周角の定理の逆より,4点A,C,D,Eは同一円周上にあることになります。このとき,△ACEの外接円は円Oであるので,点Dは円Oの円周上に存在します。つまり,4点A,B,C,Dは円Oの円周上にあることになり,四角形ABCDは円Oに内接することがわかります。
このように,1組の対角の和が180°である四角形は円に内接します。
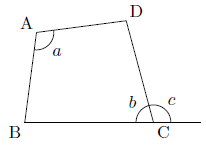
また,1つの外角がそれと隣り合う内角の対角に等しい場合についても,次の図のように,
∠a=∠c,∠b+∠c=180°
という関係から,結局
∠a+∠b=180°
のようになり,「1組の対角の和が180°である四角形」と同じ条件になるので,円に内接します。
以上のことから,内接四角形の性質の逆が成り立ち,共円条件は次のようになります。
- 1組の対角の和が180°
- 外角が,それと隣り合う内角の対角に等しい
