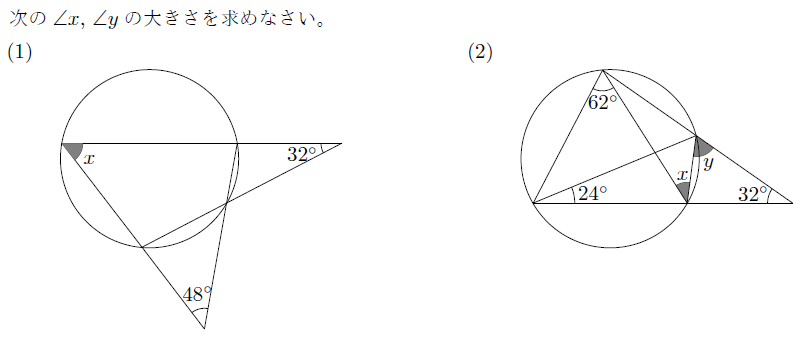
【解説】
多角形のすべての頂点が1つの円周上にあるとき,その多角形は円の内側で接するので,円に内接するといい,円は多角形の外側で接するので,多角形の外接円といいます。
ここでは,次の図のような円Oに内接する四角形ABCDについて考えます。
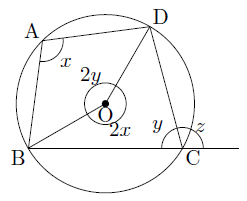
上の図のように∠A=x,∠C=yとすると,∠Aは弧BCDに対する円周角,∠Cは弧BADに対する円周角であるので,それぞれの中心角は,円周角の定理より2x,2yとなります。
このことから,
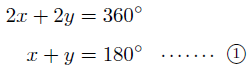
となり,円に内接する四角形の対角の和は180°になります。
また,∠Cの外角をzとすると,
y+z=180°……②
となるので,①,②よりx=zとなり,円に内接する四角形の1つの外角の大きさは,それと隣り合う内角の対角の大きさに等しいという関係も成り立ちます。
【例題】
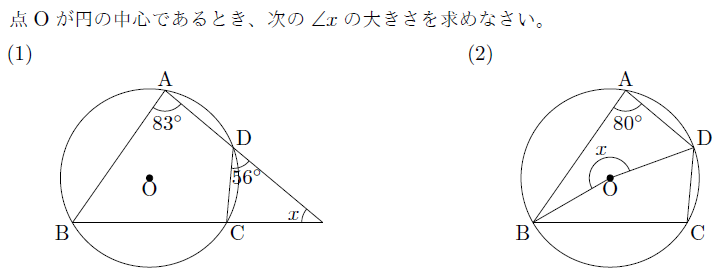
【無料動画講義(理論)】
【演習問題】