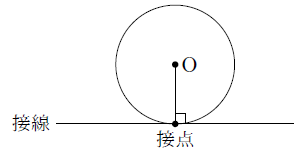
【解説】
直線と円がただ1点を共有するとき,この直線は円に接するといい,この直線を円の接線,この共有点を接点といいます。また,円の中心と接点とを結ぶ直線は,円の接線に垂直になります。
次の図のように,円Oの外部の点Pから円に接線を引くと,2本の接線を引くことができ,そのときの接点をそれぞれQ,Rとすると,円外の点Pから接点Q,Rまでの距離PQ,PRを接線の長さといいます。
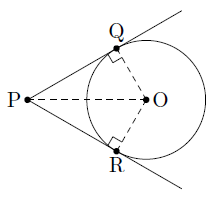
ここで,△PQOと△PROに着目すると,
∠PQO=∠PRO=90°……①
また,円の半径は等しいので,
OQ=OR……②
さらに,POは共通であるので,
PO=PO……③
①~③より,直角三角形の斜辺と他の1辺がそれぞれ等しいので△PQO≡△PROとなり,合同な図形の対応する線分の長さは等しいので,PQ=PRとなります。このことから,「円の外部の1点からその円に引いた2本の接線の長さは等しい」ということがわかります。
【例題】

【無料動画講義(理論)】
【演習問題】

