【解説】
次の図の円Oのように，
に対する中心角は1つしかありませんが，に対する円周角は無数に存在します。
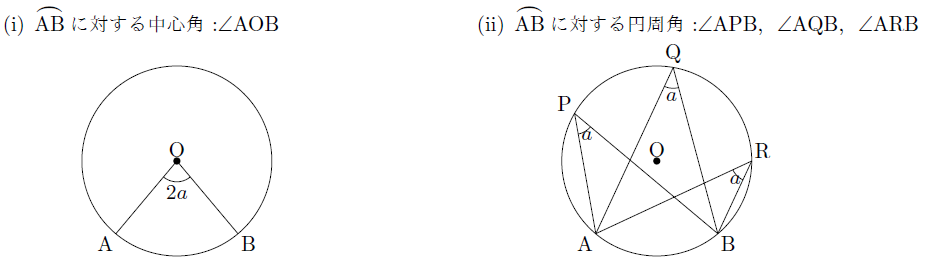
しかし，1つの弧に対する円周角は，その弧に対する中心角の1/2倍の大きさになるので，
- ∠APB=∠AOB×1/2
- ∠AQB=∠AOB×1/2
- ∠ARB=∠AOB×1/2
となります。このことから，
∠APB=∠AQB=∠ARB
となり，1つの弧に対する円周角の大きさはどれも等しくなります。このように，円周角と中心角には，
- 1つの弧に対する円周角の大きさは，その弧に対する中心角の大きさの半分になる。（1つの弧に対する中心角の大きさは，その弧に対する円周角の大きさの倍になる。）
- 同じ弧に対する円周角の大きさは等しい。
という性質があり，これを円周角の定理といいます。
【例題】
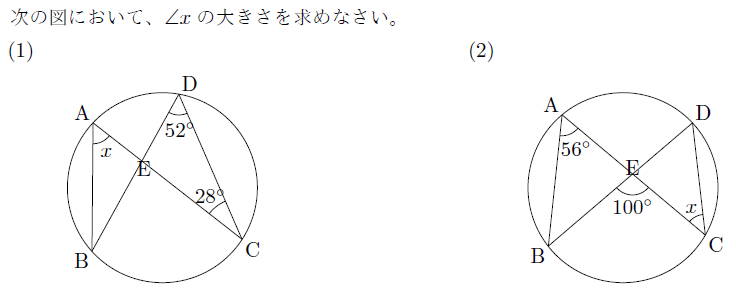
【無料動画講義（理論）】
【演習問題】
