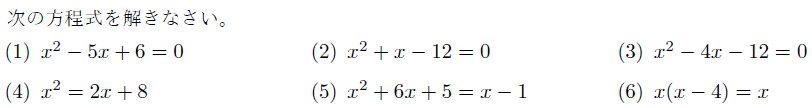【解説】
xについての2次方程式ax2+bx+c=0の左辺「ax2+bx+c」は,2次式であるので,因数分解して,
ax2+bx+c=0→( )( )=0
のような形に変形することができる場合があります。このとき,次のように,
A×B=0
という形の式が成り立つためには,
0×B=0,A×0=0,0×0=0
のように,AとBのどちらか一方,もしくは両方ともが「0」になるときしかありません。このことを数学では,
A=0 または B=0
のようにいい,この性質を利用して2次方程式を解くこともできます。
また,日常で使う「または」という言葉は,
「パンまたはライスをお選びください。」
のように,
「または」=「どちらか一方」
という意味ですが,数学の「または」という言葉は,
「または」=「どちらか一方,もしくは両方」
のように,日常使う言葉の意味と少し異なるので注意してください。
2次方程式の解法には主に,次の4つの方法があります。
- 平方根を利用する。
- 平方の形に変形(平方完成)する。
- 2次方程式の解の公式を利用する。
- 因数分解を利用する。
2次方程式の解の公式を用いれば,解のある2次方程式であればすべて解くことができますが,計算がやや面倒です。そのため,2次方程式を解くときには,まずは式の形を見て,
- 「x2=数」,「( )2=数」のような形になっている,もしくは,その形に簡単に変形できる式かをチェックし,そのような式であれば平方根を利用して解く。
- 等式の性質を利用して「ax2+bx+c=0」の形に整理し,その式の左辺が因数分解できるかどうかを確認し,できる場合には因数分解を利用して解を求める。
- 左辺が因数分解ができない場合には,解の公式を利用(もしくは,平方完成)して解を求める。
というような考えで,2次方程式に取り組むようにしてください。
ただし,2次方程式の左辺ax2+bx+cが因数分解できるかどうかは厳密に判断する必要はなく,「できそう」か,「できなさそう」かの判断で十分です。因数分解できるかどうかに悩んでしまい,解くまでに時間がかかってしまうくらいなら,少し面倒でも解の公式を利用して解いてしまったほうがいいと思います。そのため,たとえ因数分解できたとしても,自分が因数分解「できなさそう」と判断したのなら,解の公式を利用して解いてしまいましょう。
【例題】
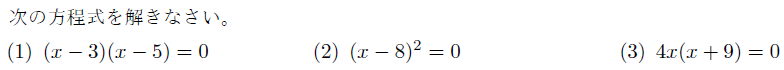
【無料動画講義(理論)】
【演習問題】