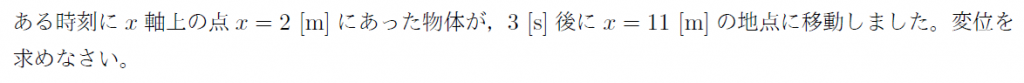【解説】
次の図のように，原点と$x$軸を描いたとき，$x$軸上を運動する物体があると，その物体の時刻$t$における位置を$x$座標を用いて表すことができます。
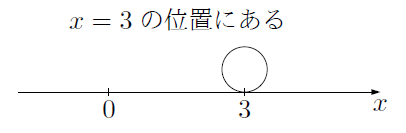
ある時刻$t_1$に位置$x_1$にあった物体が，時刻$t_2$に位置$x_2$に移動したとき，位置座標の変化量は，変化量を表す「$\Delta$（デルタ）」という記号を用いて，
$$\Delta x =x_2 -x_1$$
と表すことができ，この $\Delta x$を変位といいます。
このとき，「変化量」とは，
$$（変化量）=（変化後の値）-（変化前の値）$$
で求められる量になります。
また，変位は「向き」と「大きさ」を併せ持った量になるので，図のように矢印の向きと長さでそのようすを表すことができます。そして，変位の大きさのことを距離といいます。
【例題】
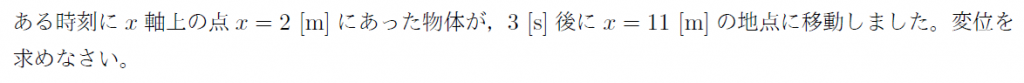
【無料動画講義（理論）】
【演習問題】
