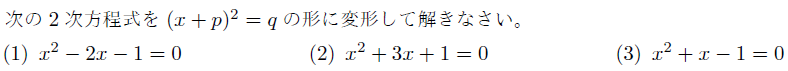【解説】
(x+p)2=qのようなxについての2次方程式は,平方根の考え方を利用して,
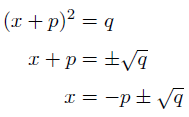
と解くことができました。このように,左辺にx2や( )2などの2乗(平方)の形があり,右辺が定数であるような2次方程式は,平方根を利用して解くことができます。そこで,2次方程式の左辺がx2や( )2などの2乗(平方)の形になっていないような場合,その2次方程式の左辺を2乗(平方)の形に変形(このことを「平方完成する」といいます)することを考えます。
(x+p)2=qの左辺を,平方公式を利用して展開すると,
x2+2px+p2=q
となります。このことから,左辺に「x2+2px+p2」という形があれば,左辺を平方公式を利用して因数分解することで,
(x+p)2=q
という,左辺に2乗(平方)のある形に変形(平方完成)することができます。そのため,平方完成は次のような手順で行うことができます。
- 定数項を右辺に移項する。
x2+2px-q=0→x2+2px=q - 「xの係数の半分の2乗」を両辺に加える。
x2+2px=q→x2+2px+p2=q+p2 - 左辺を因数分解して,平方の形にする。
x2+2px+p2=q+p2→(x+p)2=q+p2
【例題】

【無料動画講義(理論)】
【演習問題】