底辺の等しい三角形の面積比

【解説】

次の図のような△ABCと△ACDの底辺をそれぞれ，BC，CDであるとすると，2つの三角形の高さが等しくなるので，その面積比は底辺の比に等しくなり，

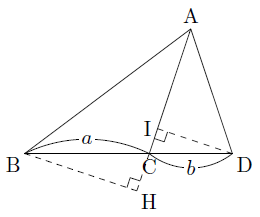
△ABC:△ACD=a:b

となりました。

ここで，点B，DからACに垂線を引き，ACまたはその延長との交点をそれぞれH，Iとします。このとき，2つの三角形の底辺をACであるとすると，△ABCと△ACDの面積比は，

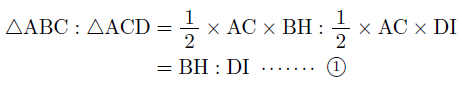
と表すことができ，底辺の等しい三角形の面積比は，高さの比に等しくなります。

また，△BHCと△DICにおいて，

∠BHC=∠DIC=90°，∠HCB=∠ICD（対頂角）

より，2組の角がそれぞれ等しいので，△BHC∽△DIC。相似な図形の対応する辺の比は等しいので，

BH:DI=BC:DC=a:b……②

となり，高さの比をa:bで表すことができます。よって，①，②より，△ABCと△ACDの面積比は，

△ABC:△ACD=a:b

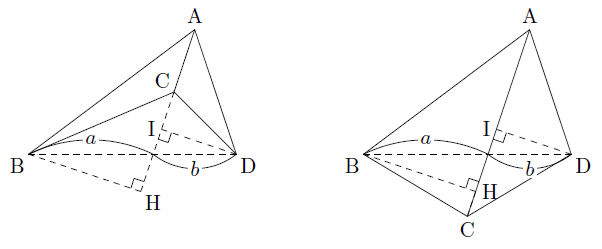
と表され，次のような図においても，底辺がACで等しいので，面積比は高さの比になり，その面積比△ABC:△ACDはすべてa:bになります。