【解説】
次の図のように,2つの線分AB,CD,またはその延長の交点をPとします。
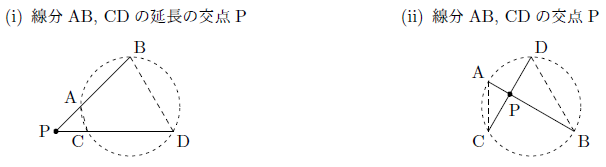
このとき,PA×PB=PC×PDであるとすると,△PACと△PDBにおいて,
PA:PD=PC:PB……①
また,
∠APC=∠DPB……②
①,②より,2組の辺の比とその間の角がそれぞれ等しいので,
△PAC∽△PDB
相似な図形の対応する角の大きさは等しいので,
∠CAP=∠BDP
となります。このことから,(i)は内接四角形の性質の逆,(ii)は円周角の定理の逆により,それぞれ4点A,B,C,Dは同一円周上にあることがわかり,方べきの定理の逆が成り立ちます。
