【解説】
測定値などの近似値において信頼のできる数字のことを有効数字といいます。
測定値などの近似値を用いて計算を行う場合,その数値には誤差が含まれるため,有効数字を考えて行う必要があります。このとき,計算途中では,最終的な有効数字の桁数よりも1桁余分にとって計算を行います。
有効数字についてのことわりがない場合には,有効数字は2桁(もしくは3桁)程度にそろえておけば問題ありません。
- 測定値どうしの加減:測定値の和・差は,測定値の末位が最も高い位のものに合わせる
例として,小数第2位までの測定値1.23と小数第1位までの測定値45.6の和を求めるとき,末位の位を低い方に無理矢理そろえて計算することを考えると,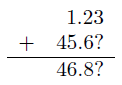
- 測定値どうしの乗除:測定値の積・商は,有効数字の桁数の最も少ないものに合わせる
有効数字3桁の測定値1.23と有効数字2桁の測定値4.5の積を求めるとき,有効数字の桁数の多い3桁に無理矢理そろえて計算すると,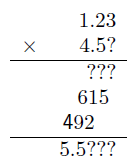
ただし,割り算が含まれる場合,割り切れれば問題ありませんが,割り切れないような数で割り算を行ってしまうと,そこで四捨五入をし,また,計算の最後で四捨五入をしなければならず,誤差が大きくなってしまいます。そのため,計算の最後に1度だけ行うようにします。
