【解説】
空間図形は苦手という人が多いと思いますが,空間図形を空間図形のまま考えると難しくなります。「直方体の対角線」では,直方体という空間図形を,△AEGと△EFGという平面図形で考えます。このように,いかにして空間図形を平面図形で考えられるようにするかが,空間図形の問題を考える上でのポイントになります。このことを念頭に置きながら問題に取り組むようにしましょう。
次の図のような直方体があります。
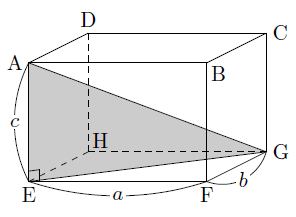
このとき,辺AEは面EFGHに垂直なので,
AE⊥EG
となり,△AEGは直角三角形になります。
そこで,△AEGに三平方の定理を用いると,
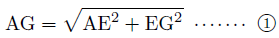
となります。
次に,△EFGに着目すると,EGは長方形EFGHの対角線なので,△EFGは直角三角形になります。
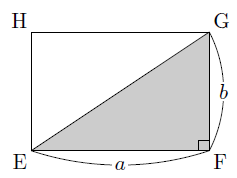
そこで,△EFGに三平方の定理を用いると,
EG2=EF2+GF2
となるので,これを①に代入すると,
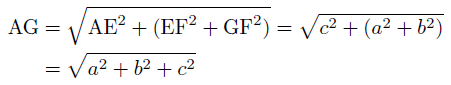
と,線分AG(直方体の対角線)の長さを求めることができます。
このことから,
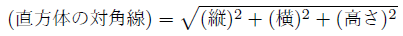
という関係が成り立つので,これを公式として利用します。
【例題】

【無料動画講義(理論)】
【演習問題】

