【解説】
次の図のように,相似な2つの三角形△ABCと△DEFの相似比がp:qであるとします。
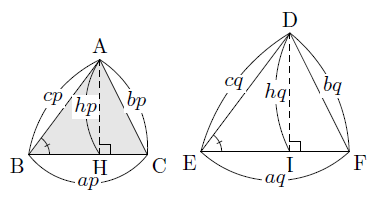
相似な2つの三角形の対応する角の大きさは等しいので,その角をそろえるように2つの三角形を重ねることができます。
そこで,2つの三角形を∠Bと∠Eをそろえるように並べると,∠B(∠E)を共有していると考えることができるので,2つの三角形の面積比は,
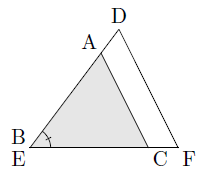
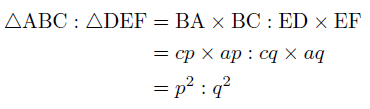
となり,相似な三角形の面積比は,相似比の2乗の比になります。
また,このことは,三角形の面積を直接求めることでも,
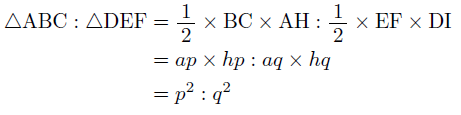
と求めることができます。
平面図形の面積は,
長方形の面積=(縦の長さ)×(横の長さ),平行四辺形の面積=(底辺の長さ)×(高さ)
などのように,2つの長さの積により求めることができるので,対応する部分の長さがk倍なら,2つの長さはそれぞれk倍され,面積はk2倍になります。つまり,相似な三角形のときだけではなく,相似な平面図形であれば,対応する部分の長さがk倍のとき,面積はk2になり,相似な図形の面積比は,相似比の2乗の比になります。
【例題】
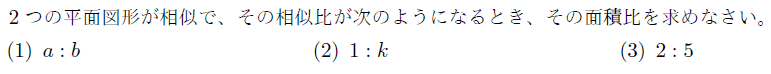
【無料動画講義(理論)】
【演習問題】

