【解説】
ある物体が直線上を一定の加速度で運動するとき,これを等加速度直線運動といいます。
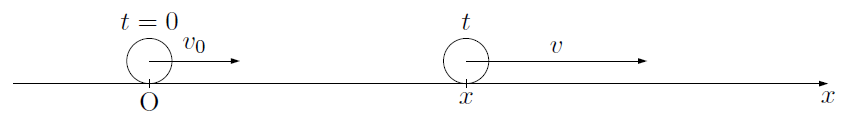
ここで,
このときの等加速度直線運動を
と表すことができます。加速度は1 [s]あたりの速度の変化量であるので,
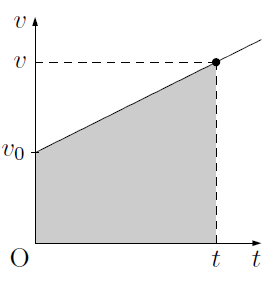
次に,時刻
と表すことができます。
また,①の式は
という関係を導き出すことができ,等加速度直線運動では①,②,③の式を利用して,位置,速度,加速度を求めることができます。
【例題】

【解説動画講義(理論)】
【解説動画講義(シミュレーション)】
【演習問題】

ある物体が直線上を一定の加速度で運動するとき,これを等加速度直線運動といいます。
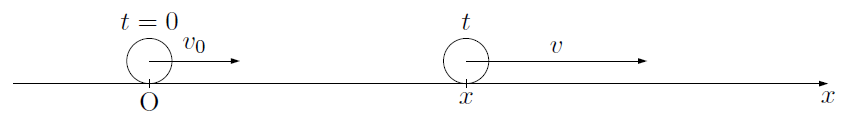
ここで,

このときの等加速度直線運動を
と表すことができます。加速度は1 [s]あたりの速度の変化量であるので,
次に,時刻
と表すことができます。
また,①の式は
という関係を導き出すことができ,等加速度直線運動では①,②,③の式を利用して,位置,速度,加速度を求めることができます。

