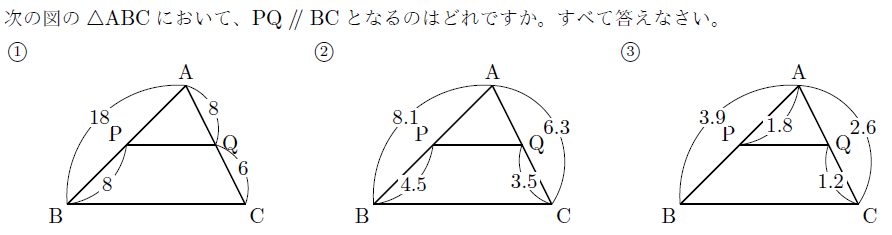
【解説】
次の図のように,△ABCの2辺AB,AC上に,それぞれ点P,Qがあるとします。
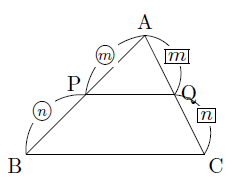
このとき,AP:AB=AQ:ACであるとすると,△APQと△ABCで,仮定より,
AP:AB=AQ:AC……①
また,∠Aは2つの三角形において共通な角であるので,
∠PAQ=∠BAC……②
①,②より,2組の辺の比とその間の角がそれぞれ等しいので,
△APQ∽△ABC
相似な図形の対応する角の大きさは等しいので,
∠APQ=∠ABC
よって,同位角が等しいので,
PQ//BC
という関係が成り立ちます。
また,AP:PB=AQ:QCであるとき,
AP:PB=AQ:QC=m:n
とすると,
AP:AB=m:(m+n),AQ:AC=m:(m+n)
よって,
AP:AB=AQ:AC
となるので,このときもPQ//BCという関係が成り立つことになります。
以上のことから,△ABCの2辺AB,AC上に,それぞれ点P,Qがあるとき,
- AP:AB=AQ:ACならばPQ//BC
- AP:PB=AQ:QCならばPQ//BC
という関係が成り立ちます。
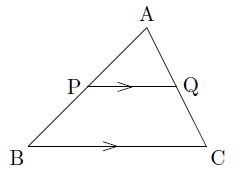
2つの直線が平行であることを示すには,「同位角や錯角が等しい」というように,「角」についての条件がほとんどでしたが,ここで学習したように,「線分の比」を利用することでも,2つの直線が平行であることを示すことができます。
【例題】
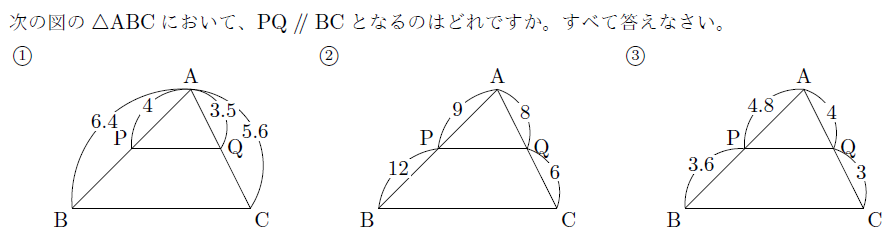
【無料動画講義(理論)】
【演習問題】