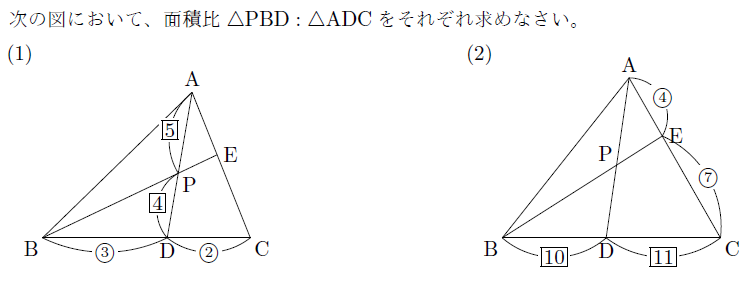
【解説】
2つの角∠A,∠Bが,∠A+∠B=180°となるとき,∠Aと∠Bは,たがいに補角の関係にあるといいます。
ここで次の図のように,1組の角(∠BCAと∠ECD)がたがいに補角をなす(∠BCA+∠ECD=180°)三角形(△ABCと△ECD)の面積比を考えます。
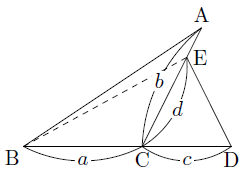
△EBCと△ECDは,底辺をそれぞれBC,CDであるとすると,2つの三角形の高さは等しいので,面積比は底辺の比に等しくなり,
△EBC:△ECD=BC:CD=a:c(=ad:cd)……①
また,△ABCと△EBCも,底辺をそれぞれCA,CEとすると,2つの三角形の高さは等しいので,面積比は底辺の比に等しくなり,
△ABC:△EBC=CA:CE=b:d(=ab:ad)……②
①,②より,
△ABC:△ECD=ab:cd
となり,1組の角がたがいに補角をなす三角形の面積比は,補角の関係にある角をはさむ2辺の積の比に等しくなります。
【例題】
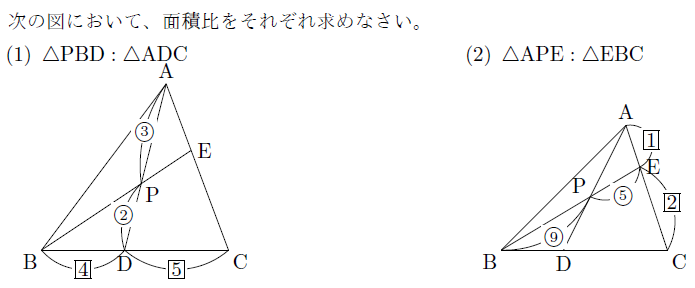
【無料動画講義(理論)】
【演習問題】