【解説】
次の図のようなすべての辺の長さがaの正三角錐(正四面体)A-BCDについて考えます。
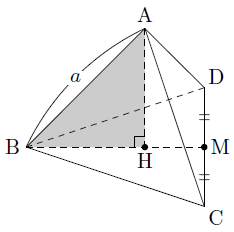
頂点Aから底面BCDに垂線AHを引くと,このAHの長さが正四面体の高さになります。このとき,図のように△ABHに着目すると直角三角形であるので,三平方の定理を利用してAHの長さを求めることができますが,その前にまずはBHの長さを求める必要があります。
正四面体A-BCDを上から見ると,次の図のように点Aと点Hが重なって見えます。
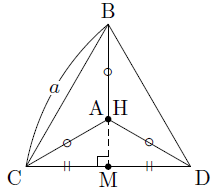
正四面体はすべての辺の長さが等しいので,AB=AC=ADであることから,
HB=HC=HD
となるはずです。このようにして,正四面体のような正多角錐の垂線の足(点H)は,底面の各頂点から等しい距離にある点(これを外心といいます)になります。また,正三角錐(正四面体)の底面は正三角形になりますが,正三角形の外心と重心(重さの中心)は一致し,重心は中線(三角形の頂点と辺の中点とを結ぶ線BM)を2:1に分割する点になります。△BCMは60°の角をもつ直角三角形なので,
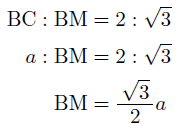
そして,BH:HM=2:1より,
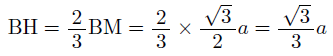
よって,△ABHに三平方の定理を利用して,正四面体の高さAHは,
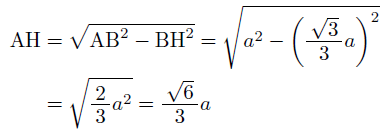
となり,正四面体の体積は,
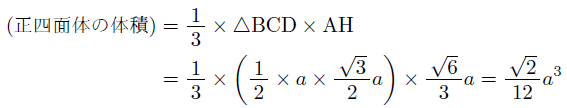
この正四面体の高さと体積を公式として利用できますが,この高さと体積を求めた考え方は,他の正多角錐の高さや体積を求めるときにも利用できるものになります。
【例題】

【無料動画講義(理論)】
【演習問題】

