次の立体の体積を求め，ア，イに当てはまる数を半角英数字で入力しなさい。

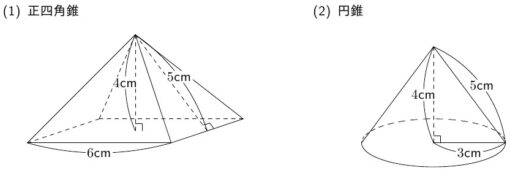
1. \( \fbox{ア} \ \text{cm}^3 \)
2. \( \fbox{イ} \ \pi \ \text{cm}^3 \)

角錐や円錐の体積は，同じ底面と高さである角柱や円柱の体積の\(\displaystyle \frac{1}{3} \)倍になります。つまり，角錐や円錐の体積は，

\begin{align}
\text{（角錐・円錐の体積）} &=\text{（角柱・円柱の体積）} \times \frac{1}{3} \\
&=\text{（底面積）} \times \text{（高さ）} \times \frac{1}{3} \end{align}

という公式で求められます。また，ここでいう「高さ」とは，「頂点から底面までの距離」になります。

三角形などの平面図形では，「高さ」と言われれば「頂点から底辺に下ろした垂線の長さ」のことで，「高さ」と「底辺」は垂直に交わっています。同じように，角錐や円錐の高さは「頂点から底面までの距離」で，「頂点から底面に下ろした垂線の長さ」になり，こちらも「高さ」と「底面」は垂直に交わっています。角柱や円柱のときと比べて，「高さ」が少しわかりにくいですが，その点に注意しながら見極められるようにしてください。