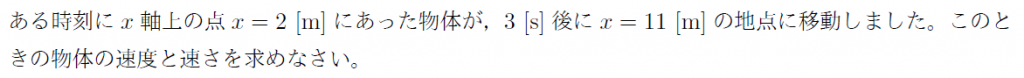【解説】
1 [s]あたりの物体の変位を速度といいます。
上の図のように，ある時刻$t_1$に位置$x_1$にあった$x$軸上を運動する物体が，時刻$t_2$に位置$x_2$に移動したとき，速度$v$（「velocity」の頭文字）は，時刻$\Delta t =t_2 -t_1$における変位が$\Delta x =x_2 -x_1$になるので，
$$v =\frac{\Delta x}{\Delta t} =\frac{x_2 -x_1}{t_2 -t_1}（単位：\text{m/s}）$$
と表すことができ，これが速度の定義式になります。
一般的に，速度は時々刻々と変化するので，上で求めた速度はその間の平均の速度になります。そこで，$\Delta t$を限りなく0に近づけると，$\displaystyle v =\frac{\Delta x}{\Delta t}$はある極限値に近づき，この極限値をその時刻における瞬間の速度（単に「速度」と言われたときは，この「瞬間の速度」を指すことが基本です）といいます。
速度は1 [s]あたりの変位であるので，変位がそうであったように，速度も「向き」と「大きさ」を併せ持ったものになるので，矢印の向きと長さでそのようすを表すことができます。そして，速度の大きさのことを速さといいます。
【例題】
【無料動画講義（理論）】
【演習問題】
