【解説】
速度は,「向き」と「大きさ」を併せ持った量(ベクトル量)であるので,矢印(有向線分)で表すことができます。
速度
とベクトルの和で表すことができ,これを合成速度といい,合成速度を求めることを速度の合成といいます。
これとは逆に,速度
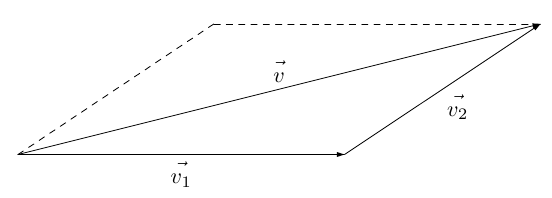
速度の合成を図で考える場合は,2つの速度を2辺とするような平行四辺形の対角線が合成速度になり,速度の分解を行うときはその逆で,速度を平行四辺形の対角線となるようにしたとき,その平行四辺形の2辺が分速度となります。ただし,速度の分解を行うときは,平行四辺形ではなく長方形で考え,分速度が直交するように考えるのが一般的です。
【例題】
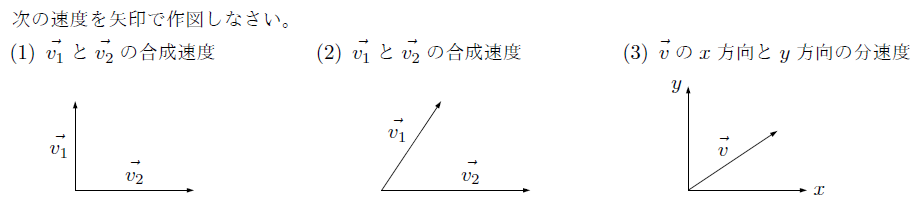
【解説動画講義(理論)】
【演習問題】

