【解説】
物体が平面上を運動する場合においても,1 [s]あたりの物体の変位が速度になります。
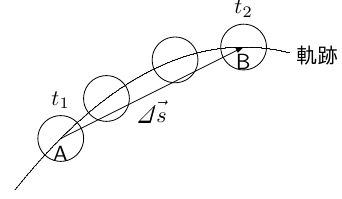
上の図のように,ある時刻
と表すことができ,これが速度の定義式になります。
このとき,
また,物体が平面上を運動する場合においても,1 [s]あたりの物体の速度の変化が加速度になり,時間
と表すことができ,これが加速度の定義式になります。
このとき,
物体が平面上を運動する場合においても,1 [s]あたりの物体の変位が速度になります。

上の図のように,ある時刻
と表すことができ,これが速度の定義式になります。
このとき,
また,物体が平面上を運動する場合においても,1 [s]あたりの物体の速度の変化が加速度になり,時間
と表すことができ,これが加速度の定義式になります。
このとき,