【解説】
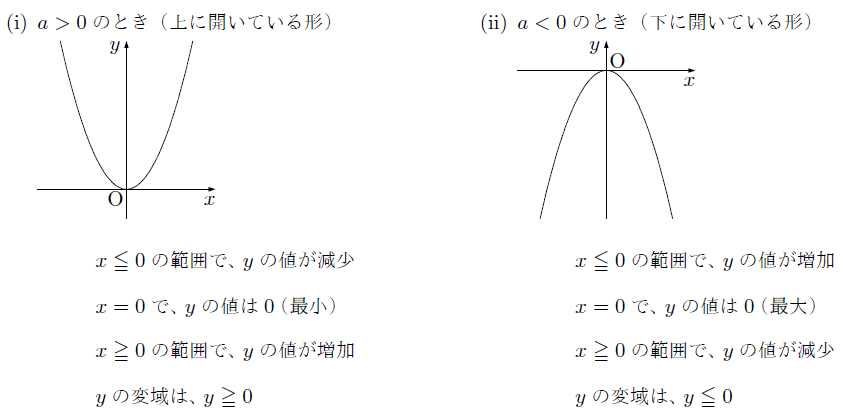
関数y=ax2のグラフには次のような特徴があります。
そのため,xの変域x1≦x≦x2において,yの変域は次のような場合が考えられます。
- a>0のとき(上に開いている形)

- a<0のとき(下に開いている形)

xの変域に制限のある関数のグラフをかくときは,xのとりうることのできる範囲のグラフを実線,それ以外の範囲のグラフはかかないでおくか,点線にしてかくようにします。
【例題】

【無料動画講義(理論)】
【演習問題】

関数y=ax2のグラフには次のような特徴があります。

そのため,xの変域x1≦x≦x2において,yの変域は次のような場合が考えられます。
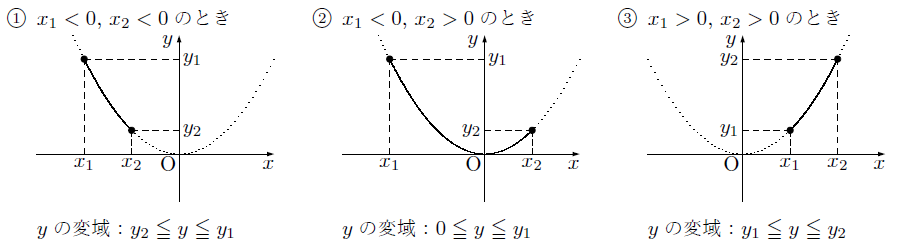
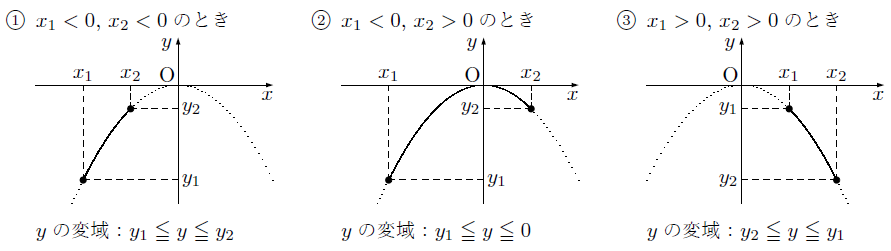
xの変域に制限のある関数のグラフをかくときは,xのとりうることのできる範囲のグラフを実線,それ以外の範囲のグラフはかかないでおくか,点線にしてかくようにします。

