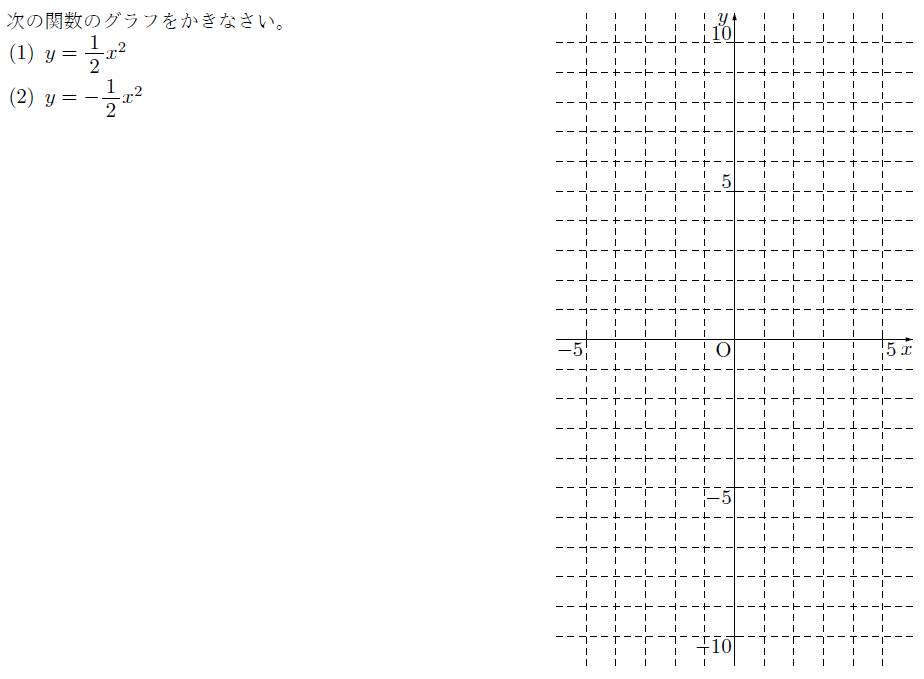
【解説】

まずは，関数y=ax²のグラフの基本となる，a=1のときのグラフ，つまり，関数y=x²のグラフについて考えていきます。

グラフをかくには，

1. xとyの対応表を完成させる。
2. 1の表から，それらに対応する点(x，y)を図にかき入れ，その点をなめらかに結ぶ。

という手順によってかくことができるので，ここでもその手順によって，関数y=x²のグラフをかいてみます。

1. xとyの対応表を完成させる。
   xの値を多く細かくすれば，それだけグラフはかきやすくはなりますが，その分手間がかかってしまうので，ここでは次のような表を作成しました。
   
   
2. 1の表から，それらに対応する点(x，y)を図にかき入れ，その点をなめらかに結ぶ。
   対応する点(x，y)を図にかき入れ，その点をなめらかに結ぶと，次のような曲線をかくことができます。
   

サッカーボールや野球のボールなど，ある物体を斜めに投げたときを考えると，その物体がたどる道筋は次のようになります。

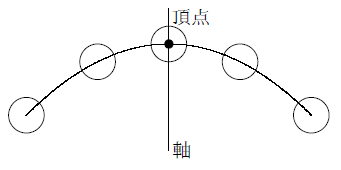
このように，「物を放ったときにできる線」を放物線といいます。関数y=ax²のグラフも上下さかさまになっていますが，同じ形なので放物線になります。

また，放物線はあるところを基準にして左右対称な形（線対称）になるため対称軸をもち，この対称軸のことを単に軸といい，対称軸と放物線の交点のことを，放物線の頂点といいます。

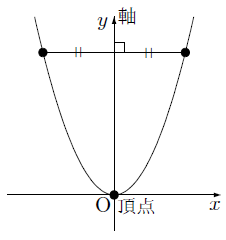
関数y=x²のグラフでは，軸はy軸，原点が頂点になります。一般的に，関数y=ax²のグラフは，「原点を通り，y軸について対称な放物線」になります。

関数y=ax²のグラフをかくときには，

1. xとyの対応表を作る。
2. 点(x，y)を図にかき入れ，その点をなめらかに結ぶ。

という手順でかくことが基本になりますが，y軸に対称なグラフになるので，次の表のようにx≧0となる部分の数値を考えて，

• 点(1，a)を図にかき入れる→その点とy軸について対称な点(-1，a)も図にかき入れる
• 点(2，4a)を図にかき入れる→その点とy軸について対称な点(-2，4a)も図にかき入れる

のように，y軸について対称になる点を合わせて図にかき入れるようにすると，効率よくグラフをかくことができます。

【例題】

【無料動画講義（理論）】