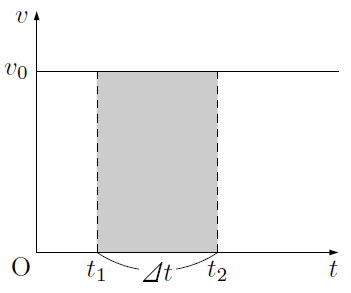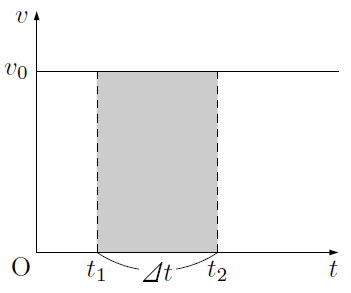v-tグラフ

【解説】

縦軸に速度$v$，横軸に時刻$t$をとって表したグラフを$v -t$グラフといいます。

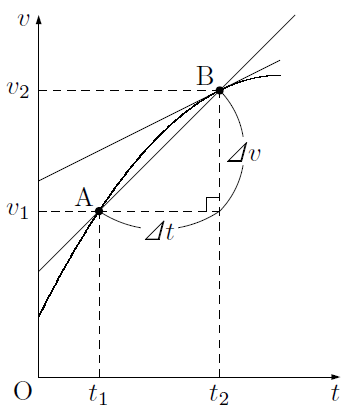
$v -t$グラフでは，ある時刻における物体の速度を知ることができるので，上の図のような$v -t$グラフにおいて，時刻$t_1$における物体の速度を$v_1$，時刻$t_2$における物体の速度を$v_2$とすると，2点A，Bを結ぶ直線の傾きは，

$$（\text{直線ABの傾き}） =\frac{v_2 -v_1}{t_2 -t_1} =\frac{\Delta v}{\Delta t} =a$$

となり，時間$\Delta t =t_2 -t_1$の平均の加速度$a$を表すことになります。

ここで，$\Delta t$を限りなく0に近づける（2点A，Bを限りなく近づける）と，2点を結ぶ直線は曲線の接線になり，その接線の傾きは，その時刻における瞬間の加速度を表すことになります。

上の図のように，速度が一定であるような$v-t$グラフでは，影の付いた部分は長方形になるので，その面積は，

$$（影の付いた部分の面積）=v_0 \times (t_2 -t_1) =v_0 \times \Delta t$$

となります。ここで，速度の定義式$\displaystyle v =\frac{\Delta x}{\Delta t}$より，

$$\Delta x =v \Delta t \longrightarrow （移動距離）=（速さ） \times（時間）$$

と表すことができるので，図の影の付いた部分の面積は$\Delta t$の間に進んだ物体の移動距離を表すことになります。

つまり，$v -t$グラフと横軸で囲まれた部分の面積は，物体の移動距離を表すことになります。（一般的に，〇-△グラフの横軸で囲まれた部分の面積は，横軸と縦軸の要素の積に相当するものになります。）このことは，$v -t$グラフがどのような曲線でも成り立ちます。さらに，$v -t$グラフの速度が負になっている部分の面積（t軸よりも下の部分の面積）を負の面積として計算すると，物体の位置を求めることができます。

これらのことから，$v -t$グラフは，物体の運動において重要な位置，速度，加速度を読み取ることができるので，よく利用されるものになります。