【解説】

縦軸に座標$x$，横軸に時刻$t$をとって表したグラフを$x-t$グラフといいます（一般的に，縦軸が〇，横軸が△となっているグラフを「〇-△グラフ」といいます）。

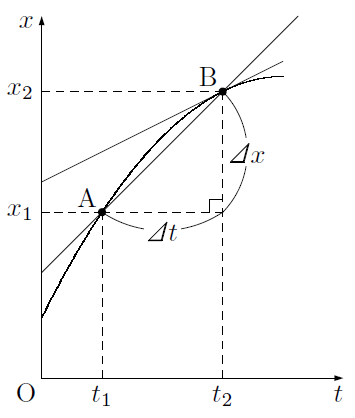
$x-t$グラフでは，ある時刻における物体の座標（位置）を知ることができるので，上の図のような$x-t$グラフにおいて，時刻$t_1$における物体の座標を$x_1$，時刻$t_2$における物体の座標を$x_2$とすると，2点A，Bを結ぶ直線の傾きは，

$$（\text{直線ABの傾き}）=\frac{x_2-x_1}{t_2-t_1}=\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}=v$$

となり，時間$\mathrm{\Delta }t=t_2-t_1$の平均の速度$v$を表します。つまり，$x-t$グラフの2点を結ぶ直線の傾きが速度$v$を表すことになります。

ここで，$\mathrm{\Delta }t$を限りなく0に近づける（2点A，Bを限りなく近づける）と，2点を結ぶ直線は曲線の接線になり，その接線の傾きは，その時刻における瞬間の速度を表すことになります。

【例題】

【解説動画講義（理論）】

【演習問題】

【解説動画講義（演習）】