【解説】
1 [s]あたりの物体の速度の変化を加速度と言います。
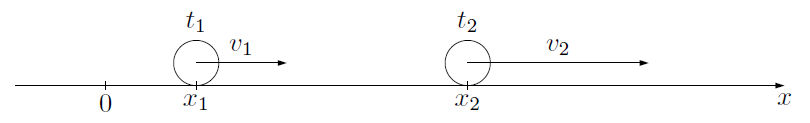
上の図のように,$x$軸上を運動する物体の時刻$t_1$のときの速度を$v_1$,時刻$t_2$のときの速度を$v_2$とすると,加速度$a$(「acceleration」の頭文字)は,時間$\Delta t =t_2 -t_1$における速度の変化が$\Delta v =v_2 -v_1$になるので,
$$a =\frac{\Delta v}{\Delta t} =\frac{v_2 -v_1}{t_2 -t_1} (単位:\text{m/s}^2)$$
と表すことができ,これが加速度の定義式になります。
一般的に,加速度も速度と同様に時々刻々と変化するので,上で求めた加速度はその間の平均の加速度になります。そこで,$\Delta t$を限りなく0に近づけると,$\displaystyle a =\frac{\Delta v}{\Delta t}$はある極限値に近づき,この極限値をその時刻における瞬間の加速度(単に「加速度」と言われたときは,この「瞬間の加速度」を指すことが基本です)といいます。
加速度は1 [s]あたりの速度の変化であるので,速度がそうであったように,加速度も「向き」と「大きさ」を併せ持ったものになります。
【例題】

【解説動画講義(理論)】
【演習問題】