次のうちの数から，無理数を(1)～(5)の記号で答えるとき，ア～ウに当てはまる数を半角英数字で入力しなさい。

1. \( \sqrt{3} \)
2. \( \sqrt{16} \)
3. \( \pi \)
4. \( 0.53 \)
5. \( -\sqrt{7} \)

\[ \textbf{無理数：}\left( \fbox{ア} \right), \ \left( \fbox{イ} \right), \ \left( \fbox{ウ} \right) \ \ \ \ \ \textbf{ただし，ア} < \textbf{イ} <\textbf{ウ} \]

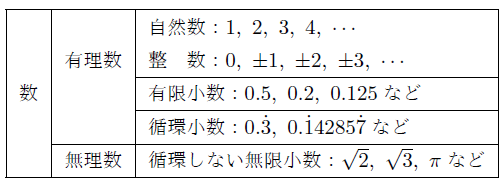
「分数で表すことのできる数」のことを有理数といいます。ここでいう「分数」とは，

\[ \textbf{分数} =\frac{\textbf{整数}}{\textbf{整数（自然数）}} \]

のような形で表される数のことです。

有限小数，循環小数は分数で表すことができることをすでに学習しましたが，自然数や整数も

\[ 2 =\frac{2}{1} \ \left( =\frac{\textbf{整数}}{\textbf{整数}} \right) \]

のように無理矢理分数で表すことができるので，自然数，整数，有限小数，循環小数が有理数になります。

また，無限小数には，あるところから同じ繰り返しになる「循環小数」がありましたが，どこまでいっても同じ繰り返しのない「循環しない無限小数」があります。しかし，この「循環しない無限小数」は，分数で表すことができないため，有理数ということはできません。このような有理数でない数のことを無理数といいます。

数の分類を表にまとめると次のようになります。