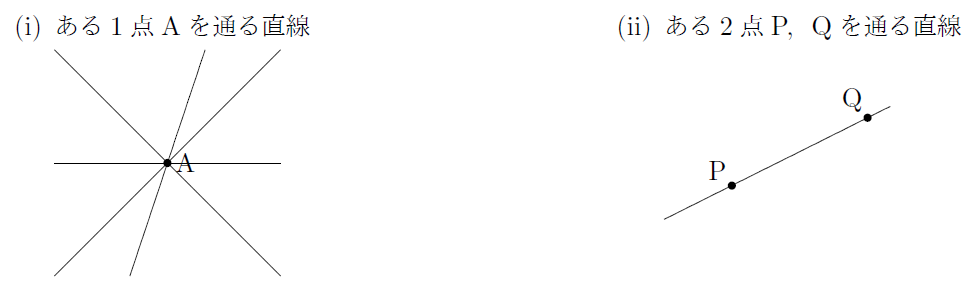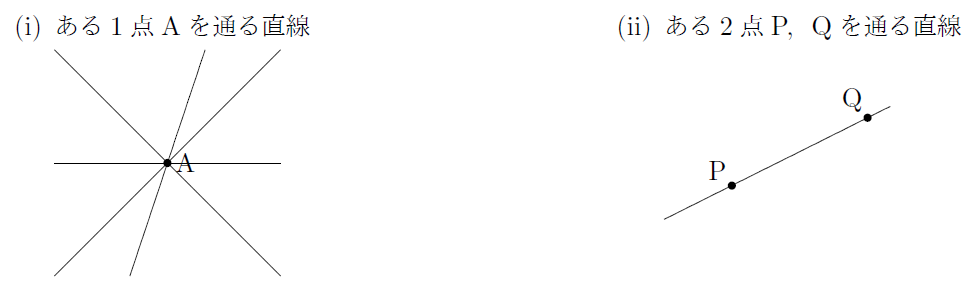,の関係を表すグラフをかくとき,基本的に次の手順でかくことができます。
- との対応表を完成させる。
- 1の表から,それらに対応する点を図にかき入れ,その点をなめらかに結ぶ。
一般に,比例のグラフは,のとき必ずになるので,原点を通る直線になります。
そして,表やグラフからもわかるように,「が1増えると,比例定数だけは増える」ので,の場合には,が1増えるごとに増加していくので右上がりのグラフ,の場合には,が1増えるごとに減少していくことになるので右下がりのグラフになります。
また,次の図のように,ある1点を通る直線はいくつも存在しますが,ある2つの点を通る直線はただ1つに決まります。

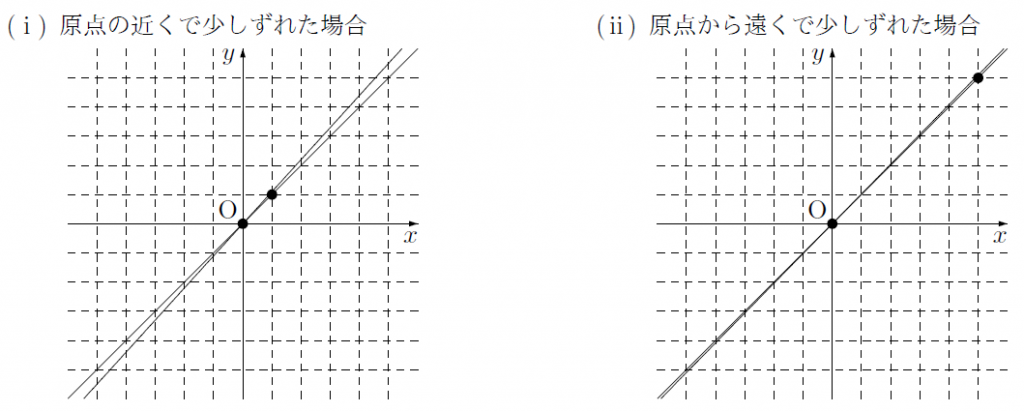
このことと,比例のグラフが「原点を通る直線」であることから,「原点」と「別のある1つの点」の2つがわかれば,その直線をかくことができます。このとき,原点以外のもう1つの点を選ぶときのポイントは,座標や座標が分数や小数だと点をかき入れにくいので,座標と座標が整数になるような点であることです。そしてさらに,原点からなるべく離れている点を選ぶことです。それは,次の図のように原点から近い点を選んだ場合,そこで少しずれてしまうと,そのずれが積み重なって,最終的には実際の直線と大きくずれてしまうことになりますが,原点から離れた点であれば,少しずれてしまっても,実際の直線とのずれも小さくすむからです。