次の立体の表面積を求め，ア，イに当てはまる数を半角英数字で入力しなさい。

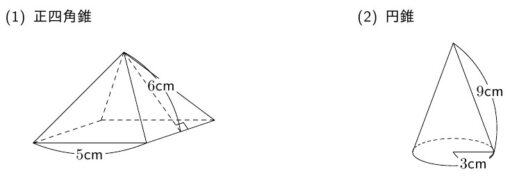
1. \( \fbox{ア} \ \text{cm}^2 \)
2. \( \fbox{イ} \ \pi \ \text{cm}^2 \)

角錐や円錐は，底面が1つなので，

\[ \text{（角錐・円錐の表面積）} =\text{（底面積）} +\text{（側面積）} \]

という計算で表面積を求めることができますが，表面積は「表面全体の面積」であるので，表面全体がわかりやすいように，見取り図から展開図を作ると考えやすくなります。

次の図のような底面の半径が\( r \)cm，母線の長さが\( R \)cmの円錐では，展開図を考えると，側面は半径\( R \)cmのおうぎ形になるので，中心角を\( x^{\circ} \)とすると，おうぎ形の弧の長さは次のように表すことができます。

\[ \text{（おうぎ形の弧の長さ）} =(2 \times \pi \times R) \times \frac{x}{360} \quad \text{（cm）} \]

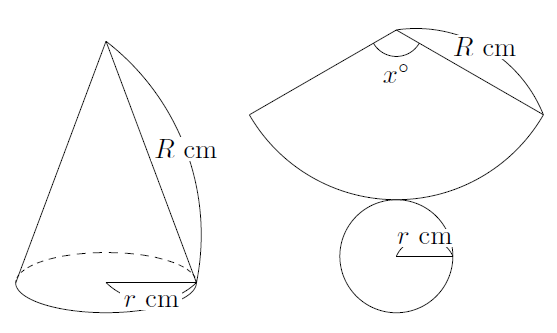
また，底面の円周の長さは，半径\( r \)cmの円なので，

\[ \text{（底面の円周の長さ）} =2 \times \pi \times r \quad \text{(cm)} \]

このとき，おうぎ形の弧の長さと底面の円周の長さは一致することから，おうぎ形の中心角は次のように表すことができます。

\begin{align}
\text{（おうぎ形の弧の長さ）} &=\text{（底面の円周の長さ）} \\
(2 \times \pi \times R) \times \frac{x}{360} &=2 \times \pi \times r \\
x &=360 \times \frac{r}{R} \\
\text{（おうぎ形の中心角）} &=360^{\circ} \times \frac{\text{底面の半径}}{\text{母線の長さ（おうぎ形の半径）}}
\end{align}

さらに，円錐の側面積であるおうぎ形の面積は次のように表され，円錐の側面積を求めるのには，この式を公式として利用します。

\begin{align}
\text{（円錐の側面積）} &=\frac{1}{2} \times \text{（おうぎ形の弧の長さ）} \times \text{（おうぎ形の半径）} \\
&=\frac{1}{2} \times \text{（底面の円周の長さ）} \times \text{（おうぎ形の半径）} \\
&=\frac{1}{2} \times 2 \pi r \times R \\
&=\pi Rr \\
&=\pi \times \text{（母線の長さ）} \times \text{（底面の半径）}
\end{align}