【講義】球の表面積と体積
- 正解率:29.63%
- 解答数:27
EXAMPLE
例題
次の半球の表面積と体積を求め,ア,イに当てはまる数を半角英数字で入力しなさい。
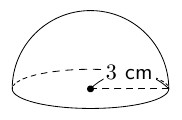
- 表面積:
- 体積:
TEXT
テキスト解説
次の図のような,中心O,半径rの球を考えます。
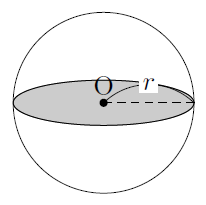
球の表面積は,球の中心Oを通る面で切ったときにできる半径
次に,半径
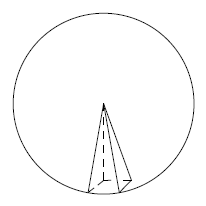
分割した角錐の体積の和が球の体積になりますが,1つ1つの角錐の体積は,
で求めることができ,角錐の高さはすべて
という関係になっています。このことから,球の体積を
MOVIE
動画解説
