【解説】
どのことがらが起こることも同じ程度であると期待されるとき,どのことがらが起こることも同様に確からしいといいます。コインを投げる場合には,コインが「表」になる場合と,「裏」になる場合がありますが,どちらが起こることも同じ程度であるので,同様に確からしいということができます。しかし,スリッパなどを投げたときに「表」になるのか「裏」になるのかを考える場合には,どちらが起こることも同じ程度というわけにはいかず,「表」になる場合が多くなってしまうので,同様に確からしいとはいえません。
起こる場合が全部でn通りあり,そのどれが起こることも同様に確からしいとします。そのうち,ことがらAの起こる場合がa通りあるとき,ことがらAの起こる確率pは,全体に対するそのことがらの割合を考えて,
ことがらAの起こる確率:p=a/n
により確率を求めることができます。
コインを1枚投げたときに表になる確率は,コインを1000回投げることで求めましたが,この式を使うと,
- すべての起こる場合の数:「表」と「裏」の2通り
- 「表」になる場合の数:1通り
より,n=2,a=1となるので,
(表になる確率)=1/2(=0.5)
と求めることができ,実験の結果と一致します。
また,
- 必ず起こることがらの確率:p=n/n=1
- 決して起こらないことがらの確率:p=0/n=0
となり,確率pの値の範囲は,
0≦p≦1
となります。
【例題】
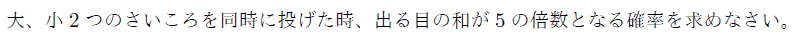
【無料動画講義(理論)】
【演習問題】

