【解説】
平面図形と同じように立体図形においても,1つの立体を形を変えずに一定の割合で拡大または縮小して得られる立体は,もとの立体と相似であるといい,もとの立体との対応する部分の長さの比を相似比といいます。
2つの相似な三角錐A-BCDとA’-B’C’D’を考え,相似比はp:qであるとします。

また,頂点A,A’から△BCD,△B’C’D’にひいた垂線をそれぞれAH,A’H’とし,三角錐A-BCD,A’-B’C’D’の体積をそれぞれV,V’とします。このとき,2つの三角錐は相似であるので,
AH:A’H’=p:q
このことから,
AH=ph,A’H’=qh
と表すことができ,また,底面の三角形も相似になるので,相似比がp:qであることから,その面積比は,
△BCD:△B’C’D’=p2:q2
となります。このことから,
△BCD=p2S,△B’C’D’=q2S
のように表すことができるので,2つの立体の体積比は,
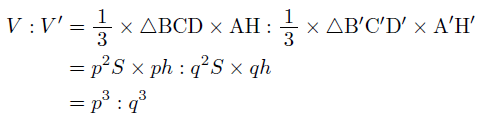
となり,相似な立体の体積比は,相似比の3乗の比になることがわかります。
面積は2つの長さの積により求めることができるので,対応する部分の長さがk倍なら,2つの長さはそれぞれk倍されて,面積はk2倍になります。しかし,立体ではさらにもう1つ長さが加わり,3つの長さの積により求めることができるので,対応する部分の長さがk倍なら,3つの長さがそれぞれk倍されて体積はk3倍になるということです。このことから,三角錐のときだけではなく,すべての相似な立体についてこの関係が成り立ちます。
【例題】
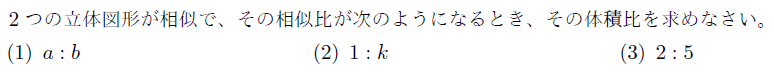
【無料動画講義(理論)】
【演習問題】

