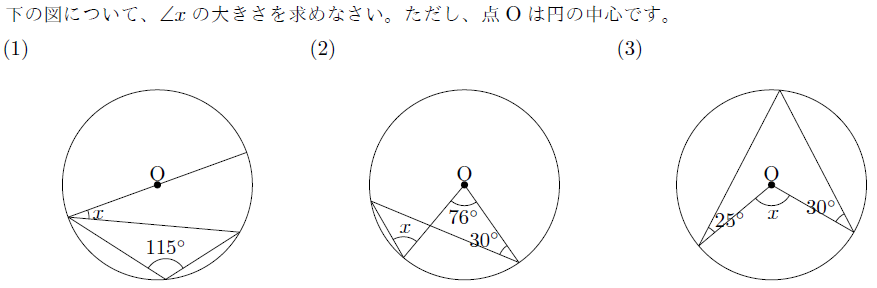
【解説】
次の図のように,円Oの円周上に3点A,B,Pをとり,その3点を結びます。
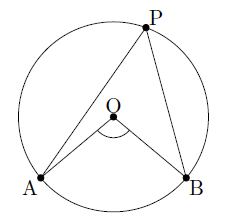
このとき,∠APBを,![]() に対する円周角といい,
に対する円周角といい,![]() を,円周角∠APBに対する弧といいます。
を,円周角∠APBに対する弧といいます。
さらに,点A,O,Bを結ぶと,おうぎ形OABを作ることができ,∠AOBを,![]() に対する中心角といいます。
に対する中心角といいます。
円周角と中心角は,
- 円周角:弧の両端の点と円周上の点を結んでできる角
- 中心角:弧の両端の点と円の中心を結んでできる角
であるので,そのことが理解できれば名前からどのような角かを判断できると思います。
ここで,点P,Oを通る直線と円Oとの交点で,点Pと異なる点をQとします。
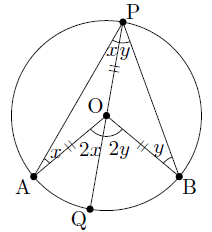
OA,OB,OPはそれぞれ円Oの半径なので,
OA=OB=OP
となり,△OPAと△OBPは二等辺三角形です。二等辺三角形の2つの底角は等しいことから,
- ∠OPA=∠OAP=x
- ∠OBP=∠OPB=y
とすると,外角の定理から,「三角形の1つの外角は,その隣にない2つの内角の和に等しい」ので,
- ∠AOQ=∠OPA+∠OAP=x+x=2x
- ∠QOB=∠OBP+∠OPB=y+y=2y
となります。
![]() に対する円周角∠APBは,
に対する円周角∠APBは,
∠APB=∠APO+∠OPB=x+y
また,![]() に対する中心角∠AOBは,
に対する中心角∠AOBは,
∠AOB=∠AOQ+∠QOB=2x+2y=2(x+y)=2∠APB
という関係が成り立ちます。つまり,
「1つの弧に対する中心角の大きさは,その弧に対する円周角の2倍の大きさになる」
ことになります。
【例題】
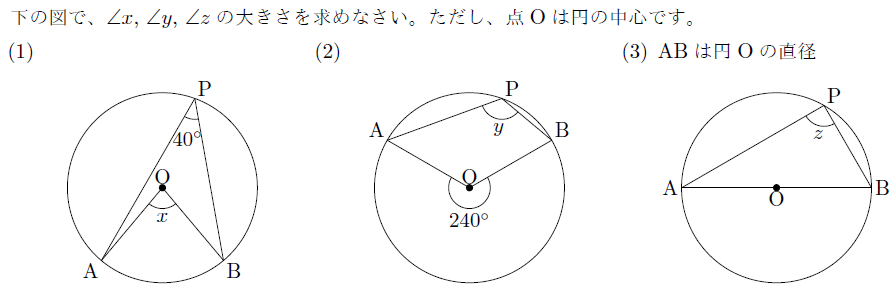
【無料動画講義(理論)】
【演習問題】