【講義】最短経路
- 正解率:33.33%
- 解答数:12
EXAMPLE
例題
次の図のような碁盤の目になっている道を,Aを出発点として,遠まわりをせずにB地点に向かいます。このとき,次の道順は何通りありますか。次のア,イに当てはまる数を半角英数字で入力しなさい。
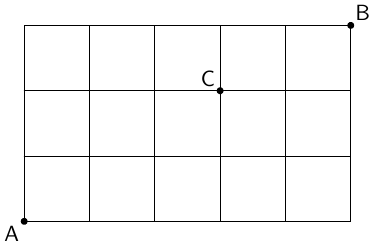
- すべての道順:
- (1)のうちで,C地点を通る道順:
TEXT
テキスト解説
次の図のような碁盤の目になっている道を,A地点からB地点まで向かうときの最短経路について考えます。
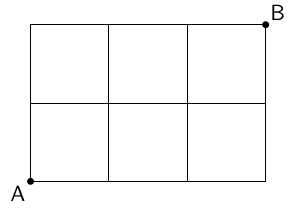
遠まわりをせずにA地点からB地点へ向かう場合,「右右右上上」,「右上右上右」,
のようにして求めることができます。
また,最短経路の総数は,各交差点で,そこにたどり着くまでの経路の数を順にかき入れていく方法でも求めることができます(動画講義参照)。この経路の数を書き込む方法は,すべてのパターンが網羅されており,また,様々な道に対応できるので是非マスターしてください。
MOVIE
動画解説
